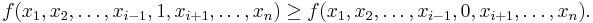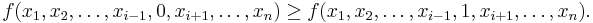Unate function

A unate function is a type of boolean function which has monotonic properties. They have been studied extensively in switching theory.

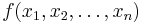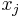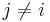
A function $f(x_1,x_2,\ldots,x_n)$ is said to be positive unate in $x_i$ if for all $x_j$ , $j\neq i$

$f(x_1,x_2,\ldots,x_{i-1},1,x_{i%2B1},\ldots,x_n) \ge f(x_1,x_2,\ldots,x_{i-1},0,x_{i%2B1},\ldots,x_n).\,$

Likewise, it is negative unate in $x_i$ if

$f(x_1,x_2,\ldots,x_{i-1},0,x_{i%2B1},\ldots,x_n) \ge f(x_1,x_2,\ldots,x_{i-1},1,x_{i%2B1},\ldots,x_n).\,$

If for every $x_i$ f is either positive or negative unate in the variable $x_i$ then it is said to be unate. A function is binate if it is not unate.

For example the Logical disjunction function or with boolean values are used for true (1) and false (0) is positive unate.

NB: positive unateness can also be considered as passing the same slope (no change in the input) and negative unate is passing the opposite slope.... non unate is dependence on more than one input (of same or different slopes)